【正确答案】:
二次型f的矩阵为 ,先求特征值和特征向量
,先求特征值和特征向量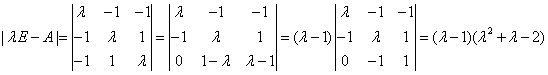 =
=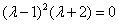 得特征值λ1=-2,λ2=-λ3=1。当λ1=-2时,特征向量满足
得特征值λ1=-2,λ2=-λ3=1。当λ1=-2时,特征向量满足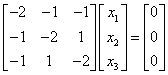 ,解得
,解得
 ;当λ2=-λ3=1时,特征向量满足
;当λ2=-λ3=1时,特征向量满足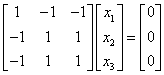 ,解得
,解得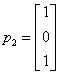 ,
,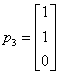 。施密特正交化如下
。施密特正交化如下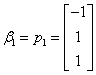 ,
, ,
,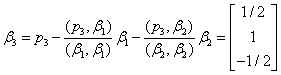 再单位化
再单位化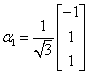 ,
,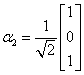 ,
, ,得
,得 ,有
,有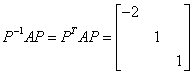 ,从而Y=P-1X,其中
,从而Y=P-1X,其中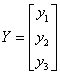 ,
,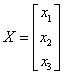 。
。
二次型f的矩阵为 ,先求特征值和特征向量
,先求特征值和特征向量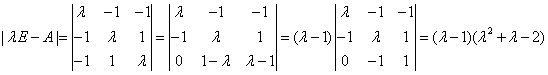 =
=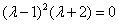 得特征值λ1=-2,λ2=-λ3=1。当λ1=-2时,特征向量满足
得特征值λ1=-2,λ2=-λ3=1。当λ1=-2时,特征向量满足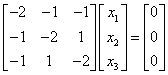 ,解得
,解得
 ;当λ2=-λ3=1时,特征向量满足
;当λ2=-λ3=1时,特征向量满足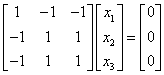 ,解得
,解得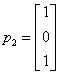 ,
,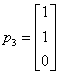 。施密特正交化如下
。施密特正交化如下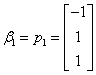 ,
, ,
,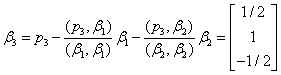 再单位化
再单位化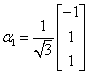 ,
,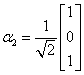 ,
, ,得
,得 ,有
,有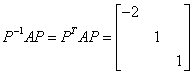 ,从而Y=P-1X,其中
,从而Y=P-1X,其中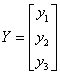 ,
,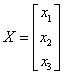 。
。
📱 扫码体验刷题小程序

扫一扫使用我们的微信小程序