设三阶矩阵A=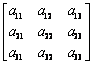
的行列式不等于0，证明：
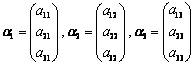线性无关．
【正确答案】：
构造齐次线性方程组Ax＝0，即（
，
，
）
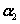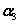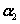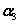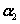＝0，x1+ x2+ x3＝0， 由已知A的行列式不等于0，根据克莱默法则，方程组有惟一零解，即当且仅当x1＝x2＝x3＝0时， x1+ x2+ x3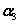＝0 成了，所以向量组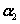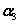，，线性无关
【题目解析】：
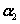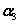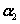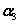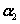构造齐次线性方程组Ax＝0，即（，，）＝0，x1+ x2+ x3＝0， 由已知A的行列式不等于0，根据克莱默法则，方程组有惟一零解，即当且仅当x1＝x2＝x3＝0时， x1+ x2+ x3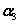＝0 成了，所以向量组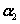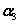，，线性无关
